What are Sequence-to-Sequence models?
Sequence-to-Sequence (Seq2Seq) models are a type of neural network architecture used for natural language processing tasks, such as machine translation, text summarization, and conversational modeling. The basic idea behind Seq2Seq models is to map a variable-length input sequence to a variable-length output sequence.
Seq2Seq models consist of two parts: an encoder and a decoder. The encoder takes an input sequence, such as a sentence, and generates a fixed-length representation of it, called the context vector. The decoder then takes the context vector as input and generates the output sequence, such as a translation of the input sentence into another language. Both encoder and decoder contain multiple recurrent units that take one element as input. The encoder processes the input sequence one word at a time and generates a hidden state h_i for each timestep i. Finally, it passes the last hidden state h_n to the decoder, which uses it as the initial state to generate the output sequence.
In a Seq2Seq model, the hidden state refers to the internal representation of the input sequence that is generated by the recurrent units in the encoder or decoder. The hidden state is a vector of numbers that represents the “memory” of the recurrent unit at each timestep.
Let’s consider a simple recurrent unit, such as the Long Short-Term Memory (LSTM) cell. An LSTM cell takes as input the current input vector x_t and the previous hidden state h_{t-1}, and produces the current hidden state h_t as output. The LSTM cell can be represented mathematically as follows:
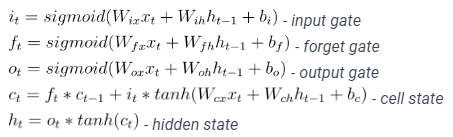
Here, W_{ix}, W_{ih}, W_{fx}, W_{fh}, W_{ox}, W_{oh}, W_{cx}, and W_{ch} are weight matrices, b_i, b_f, b_o, and b_c are bias vectors, sigmoid is the sigmoid activation function, and tanh is the hyperbolic tangent activation function.
At each timestep t, the LSTM cell computes the input gate i_t, forget gate f_t, output gate o_t, and cell state c_t based on the current input x_t and the previous hidden state h_{t-1}. The current hidden state h_t is then computed based on the current cell state c_t and the output gate o_t. In this way, the hidden state h_t represents the internal memory of the LSTM cell at each timestep t. It contains information about the current input x_t as well as the previous inputs and hidden states, which allows the LSTM cell to maintain a “memory” of the input sequence as it is processed by the encoder or decoder.
Encoder and decoder
The Seq2Seq model consists of two parts: an encoder and a decoder. Both of these parts contain multiple recurrent units that take one element as input. The encoder processes the input sequence one word at a time and generates a hidden state h_i for each timestep i. Finally, it passes the last hidden state h_n to the decoder, which uses it as the initial state to generate the output sequence.
The final hidden state of the encoder represents the entire input sequence as a fixed-length vector. This fixed-length vector serves as a summary of the input sequence and is passed on to the decoder to generate the output sequence. The purpose of this fixed-length vector is to capture all the relevant information about the input sequence in a condensed form that can be easily used by the decoder. By encoding the input sequence into a fixed-length vector, the Seq2Seq model can handle input sequences of variable length and generate output sequences of variable length.
The decoder takes the fixed-length vector representation of the input sequence, called the context vector, and uses it as the initial hidden state s_0 to generate the output sequence. At each timestep t, the decoder produces an output y_t and an updated hidden state s_t based on the previous output and hidden state. This can be represented mathematically using linear algebra as follows:

Here, W_s, U_s, and V_s are weight matrices, b_s is a bias vector, c is the context vector (from the encoder), and f and g are activation functions. The decoder uses the previous output y_{t-1} and hidden state s_{t-1} as input to compute the updated hidden state s_t, which depends on the current input and the context vector. The updated hidden state s_t is then used to compute the current output y_t, which depends on the updated hidden state s_t. By iteratively updating the hidden state and producing outputs at each timestep, the decoder can generate a sequence of outputs that is conditioned on the input sequence and the context vector.
What is the context vector, where does it come from?
In a Seq2Seq model, the context vector is a fixed-length vector representation of the input sequence that is used by the decoder to generate the output sequence. The context vector is computed by the encoder and is passed on to the decoder as the final hidden state of the encoder.
What is a transformer? How is are decoders encoders used in transformers?
The Transformer architecture consists of an encoder and a decoder, similar to the Seq2Seq model. However, unlike the Seq2Seq model, the Transformer does not use recurrent neural networks (RNNs) to process the input sequence. Instead, it uses a self-attention mechanism that allows the model to attend to different parts of the input sequence at each layer.
In the Transformer architecture, both the encoder and the decoder are composed of multiple layers of self-attention and feedforward neural networks. The encoder takes the input sequence as input and generates a sequence of hidden representations, while the decoder takes the output sequence as input and generates a sequence of hidden representations that are conditioned on the input sequence and previous outputs.
Traditional Seq2Seq vs. attention-based models
In traditional Seq2Seq models, the encoder compresses the input sequence into a single fixed-length vector, which is then used as the initial hidden state of the decoder. However, in some more recent Seq2Seq models, such as the attention-based models, the encoder computes a context vector c_i for each output timestep i, which summarizes the relevant information from the input sequence that is needed for generating the output at that timestep.
The decoder then uses the context vector c_i along with the previous hidden state s_i-1 to generate the output for the current timestep i. This allows the decoder to focus on different parts of the input sequence at different timesteps and generate more accurate and informative outputs.
The context vector c_i is computed by taking a weighted sum of the encoder’s hidden states, where the weights are learned during training based on the decoder’s current state and the input sequence. This means that the context vector c_i is different for each output timestep i, allowing the decoder to attend to different parts of the input sequence as needed. The context vector c_i can be expressed mathematically as:

where i is the current timestep of the decoder and j indexes the hidden states of the encoder. The attention weights α_ij are calculated using an alignment model, which is typically a feedforward neural network (FFNN) parametrized by learnable weights. The alignment model takes as input the previous hidden state s_i-1 of the decoder and the current hidden state h_j of the encoder, and produces a scalar score e_ij:

where a is the alignment model. The scores are then normalized using the softmax function to obtain the attention weights α_ij:

where k indexes the hidden states of the encoder.
The attention weights α_ij reflect the importance of each hidden state h_i with respect to the previous hidden state s_i-1 in generating the output y_i. The higher the attention weight α_ij, the more important the corresponding hidden state h_i is for generating the output at the current timestep i. By computing a context vector c_i as a weighted sum of the encoder’s hidden states, the decoder is able to attend to different parts of the input sequence at different timesteps and generate more accurate and informative outputs.
The difference between context vector in Seq2Seq and context vector in attention
In a traditional Seq2Seq model, the encoder compresses the input sequence into a fixed-length vector, which is then used as the initial hidden state of the decoder. The decoder then generates the output sequence word by word, conditioned on the input and the previous output words. The fixed-length vector essentially contains all the information of the input sequence, and the decoder needs to rely solely on it to generate the output sequence. This can be expressed mathematically as:
c = h_n
where c is the fixed-length vector representing the input sequence, and h_n is the final hidden state of the encoder.
In an attention-based Seq2Seq model, the encoder computes a context vector c for each output timestep i, which summarizes the relevant information from the input sequence that is needed for generating the output at that timestep. The context vector is a weighted sum of the encoder’s hidden states, where the weights are learned during training based on the decoder’s current state and the input sequence.
The attention mechanism allows the decoder to choose which aspects of the input sequence to give attention to, rather than requiring the encoder to compress all the information into a single vector and transferring it to the decoder.



